Using finite differences to solve an equations is quick and easy, especially for ODEs. On the boundaries it is not possible to use the same scheme as in the bulk and hence the boundaries need to be treated separately.  I have read several times that, at the boundary, one can use  a  lower order finite difference approximation. However, I could never find a rigorous source and it might have been for a specific equations, so here a quick try.

Let’s use the Poisson equation $\frac{d^{2}u}{d{x}^2}=0$ with the boundary conditions $u(x=0)=0$ and $\frac{du(x=1)}{dx}=1$. Using the method of manufactured solution with $u=1/6\ast x^6$  yields $\frac{d^{2}u}{d{x}^2}=5\ast x^4$.

The finite difference scheme inside the domain is 4th order and the only thing changed is the order of the finite difference scheme at the boundary $u=1$. The results for various grid spacing are below. If the order of the boundary does not affect the system, we would expect the error (the norm of the residue here) to reduce as $h^4$ where $h$ is the distance between points.

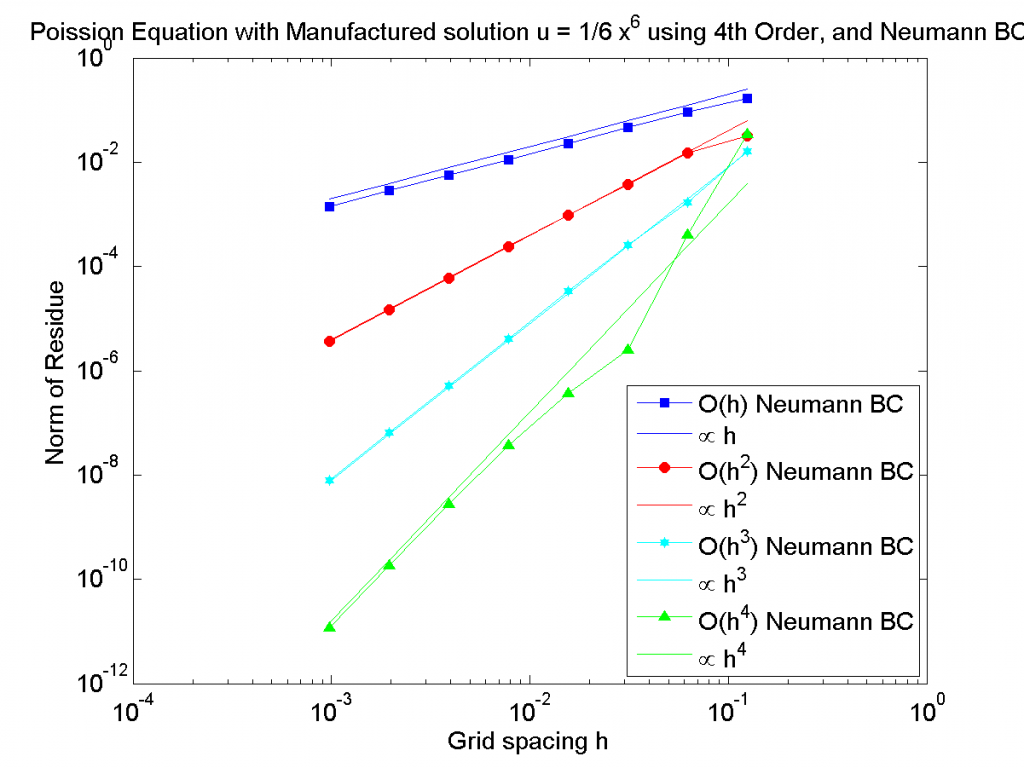
Norm of the Residue for different grid spacing. The order of the finite difference scheme at the boundary determines the order of the whole finite difference scheme.

Using a lower order finite difference approximation order at the boundary lowers the overall order of the scheme. While  this is not a full treatment of the topic it shows that in general, using lower order at the boundary will affect the overall order of your system.