What is the accuracy of centroid extracted from an image? I recently had a argument with a colleague of mine. Here a  simple test. First generate images with a sphere $n$ pixels in diameter, moving across an image. Then measure the centroid using OpenCV in Python. To keep things simple, I will move the spheres in the x-direction and only measure the x-position. To generate the images, I coloured all pixels whose central coordinate is within the radius of the centre white. The way I wrote the code induced a half-pixel offset between set and measured centroid. This gives the following image sequences:

Diameter = 3 pixels

Diameter = 5 pixelsDiameter = 20 pixels

Diameter = 50 pixels

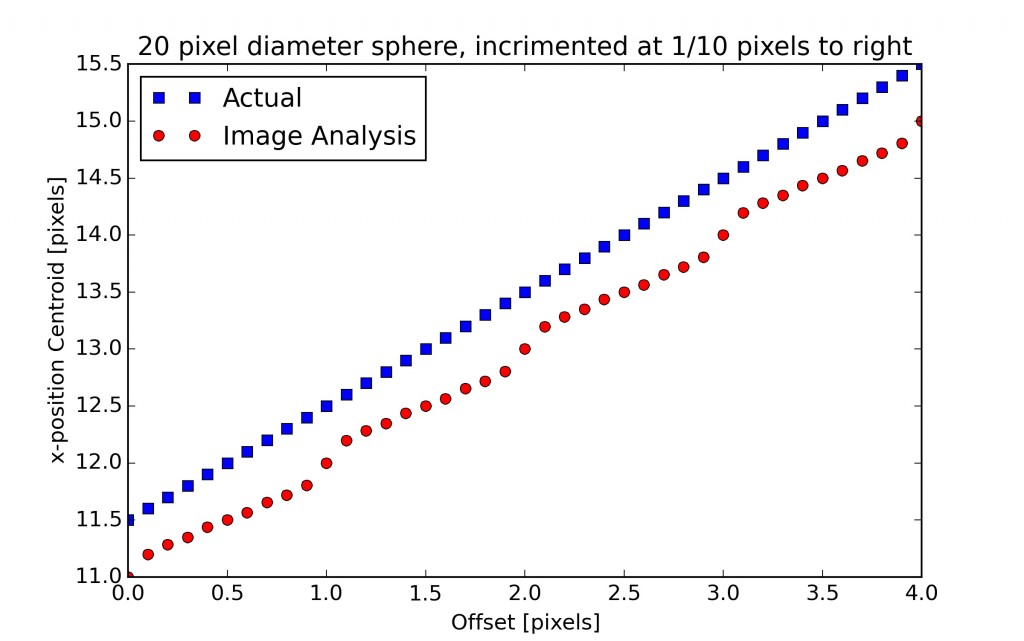
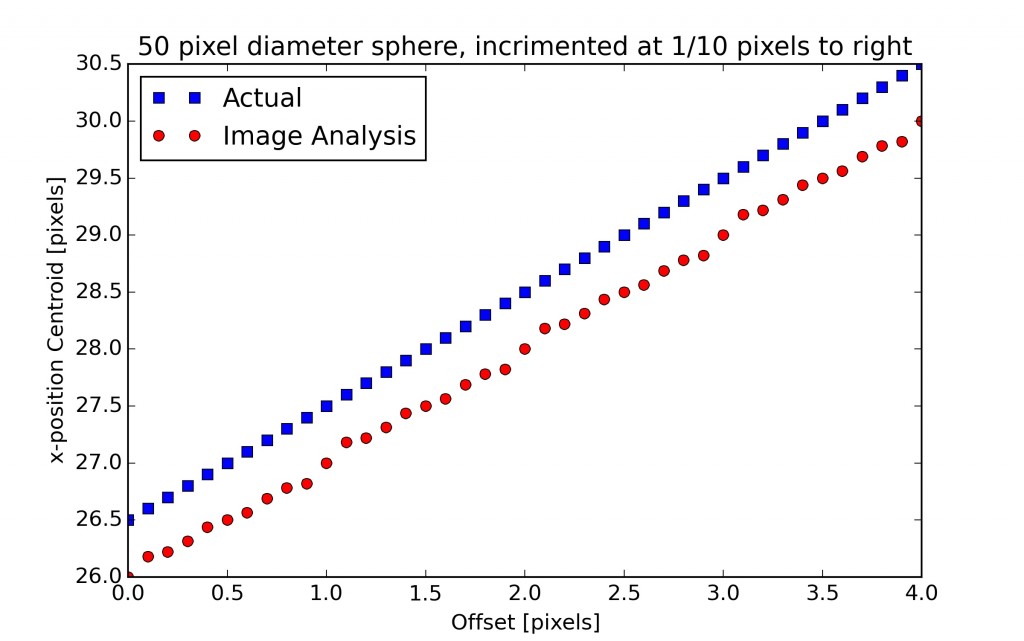
Extracting the centroid from these images results in the graphs below. We see that even for as little as 20 pixels diameter, we can get reliable sub-pixel resolution. Given that most images will at the very least be grey scale, this is also a worst case scenario. By e.g. fitting a Gaussian distribution to the  outline, we can get sub-pixel resolution on the outline itself, which will make the centroid even more accurate.

The Code:

(Can be downloaded from here.)

from __future__ import absolute_import, division, print_function
import numpy as np
import matplotlib.pyplot as plt
import os
import cv2

def drawCircle(offset = 0.0, pixelsPerDiameter=1):
'''Draw a circle with given number of pixels across with a given offset in
the x-direction. '''

h, w = int(2*pixelsPerDiameter+10), int(pixelsPerDiameter +4)
img = np.zeros((w,h), np.uint8)

#Walk through every pixel and set relevant ones to zero
centre_x = pixelsPerDiameter/2.0 +1.5
centre_y = pixelsPerDiameter/2.0 +1.5 + offset
for x in range(w):
    for y in range(h):
        r = np.sqrt((centre_x - (x+0.5))**2 + (centre_y - (y+0.5))**2)
        if r <= pixelsPerDiameter/2.0:         img[x,y] = 254 return img, centre_y, centre_x def findCentroidOpenCV(img): '''Find contours and return centroid position''' contours, hierarchy = cv2.findContours(img,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE) centroid_x, centroid_y = -1, -1 if len(contours) > 0:
    M = cv2.moments(contours[0])

    if M['m00'] == 0 or M['m10'] == 0 or M['m01'] == 0:
        print('%f, %f, %f' %(M['m00'], M['m10'], M['m01']))
    else:
        centroid_x = float(M['m10']/M['m00'])
        centroid_y = float(M['m01']/M['m00'])

return centroid_x, centroid_y

def runTest(diameter=10.0, maxOffset=21, increment=10.0):
'''Generate images and the find centroid for various offsets'''
c_x = []; c_y = []; fc_x=[]; fc_y= []; offset=[]
for ii in range(maxOffset):
    offset.append(ii/increment)
    img, centre_x, centre_y = drawCircle(offset = offset[ii], pixelsPerDiameter=diameter)

    path =''
    savepath1=path +'Pixelation'
    if not os.path.exists(savepath1): os.makedirs(savepath1)

    pathFile2=os.path.join(path, 'Pixelation', 'Size_%d_Offset_%.2f.jpg' %(diameter, offset[ii]))
    cv2.imwrite(pathFile2, img)
    centroid_x, centroid_y = findCentroidOpenCV(img)

    c_x.append(centre_x)
    c_y.append(centre_y)
    fc_x.append(centroid_x)
    fc_y.append(centroid_y)

fig = plt.figure(figsize=(8, 6), dpi=200,); ax = fig.add_subplot(111)
plt.plot(c_x, c_y, 'sb', linestyle='None', label='Actual')
plt.plot( fc_x, fc_y, 'or', linestyle='None', label='Image Analysis')
plt.show()
plt.xlabel('x-Poistion [pixels]')
plt.ylabel('y-Poistion [pixels]')
plt.title('%d pixel diameter sphere, incrimented at 1/%.f pixels to right' %(diameter, increment))
plt.legend(loc='best')

fig = plt.figure(figsize=(8, 6), dpi=200,); ax = fig.add_subplot(111)
plt.plot(offset, c_x, 'sb', linestyle='None', label='Actual')
plt.plot(offset, fc_x, 'or', linestyle='None', label='Image Analysis')
plt.show()
plt.xlabel('Offset [pixels]')
plt.ylabel('x-position Centroid [pixels]')
plt.title('%d pixel diameter sphere, incrimented at 1/%.f pixels to right' %(diameter, increment))
plt.legend(loc='best')
pathFile=os.path.join(path, 'Pixelation', 'Plot_Size_%d_Increment_%.2f_Steps=%d.jpg' %(diameter, increment, maxOffset))
plt.savefig(pathFile, dpi=300)